기울기 소실(Vanishing Gradient)은 깊은 신경망, 특히 매우 깊은 구조를 가진 신경망을 학습할 때 흔히 발생하는 문제입니다. 이로 인해 모델이 학습 과정에서 데이터로부터 제대로 학습하는 것이 어려워집니다.
기울기 소실 문제란?
딥러닝에서는 역전파(backpropagation) 라는 방법을 통해 학습이 이루어집니다. 이 과정에서 모델은 손실 함수(loss function) 를 각 가중치에 대해 미분한 기울기(일종의 변화율) 를 이용해 가중치를 조정합니다. 이 기울기는 각 가중치를 얼마나 변경해야 성능이 향상될지를 모델에게 알려줍니다. 하지만 딥 뉴럴 네트워크에서는, 역전파가 진행될수록 기울기가 점점 작아질 수 있습니다. 이러한 현상을 기울기 소실(vanishing gradient) 이라고 부릅니다.
그 결과:
- 입력에 가까운 초반 층들은 거의 업데이트를 받지 못하게 됩니다.
- 네트워크는 학습을 멈추거나 매우 느리게 학습하게 됩니다.
언제 기울기 소실이 발생하는가?
- 매우 깊은 네트워크(Very Deep Networks): 층이 많아질수록, 역전파 과정에서 기울기가 점점 작아질 가능성이 커집니다.
- 활성화 함수(Activation Functions):
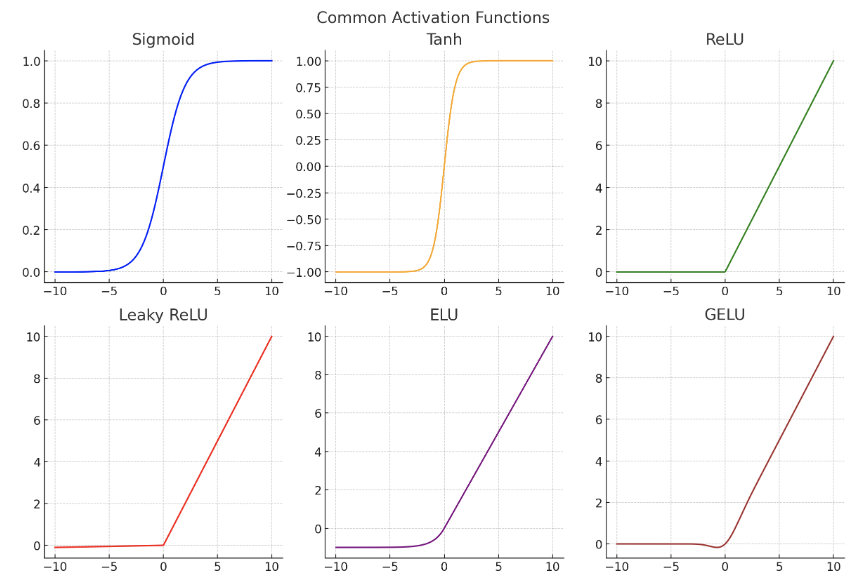
- 시그모이드(sigmoid)나 하이퍼볼릭 탄젠트(tanh) 같은 함수들은 입력 값을 작은 범위로 압축합니다
(예: 시그모이드는 입력을 0과 1 사이로 압축). - 이 함수들의 미분값(derivative) 도 매우 작습니다.
- 작은 수를 여러 번 곱하면 결과는 더욱 작아지게 됩니다.
- 시그모이드(sigmoid)나 하이퍼볼릭 탄젠트(tanh) 같은 함수들은 입력 값을 작은 범위로 압축합니다
예제:
예를 들어, 10개의 층이 있다고 가정해봅시다. 그리고 각 층에서의 기울기가 약 0.5 정도라고 할 때, 10개 층을 지나고 나면:
Final gradient = 0.5^10 = 0.000976이 매우 작은 수치는 초반 층들에서 거의 학습이 이루어지지 않는다는 것을 의미합니다.
이 문제를 어떻게 해결할 수 있나?
1. ReLU 활성함수 사용
- ReLU (Rectified Linear Unit): f(x) = max(0, x)
- ReLU 함수의 미분값은 양의 입력일 때 1, 음의 입력일 때 0입니다.
- 시그모이드 함수처럼 기울기가 작아지는 현상은 발생하지 않습니다.
PyTorch 예제:
변경전:
x = torch.sigmoid(linear(x))
변경후:
x = torch.relu(linear(x))다른 ReLU 변형들: LeakyReLU, ELU, GELU (transformer에서 주로 사용).
2. Batch Normalization 사용
- 이 기술은 각 층에 들어가는 입력을 정규화(normalization) 합니다.
- 이를 통해 기울기가 안정적인 범위 내에 머무르도록 도와줍니다.
- 또한 학습 속도와 성능을 모두 향상시키는 경우가 많습니다.
PyTorch 예제:
nn.Sequential( nn.Linear(128, 64), nn.BatchNorm1d(64), nn.ReLU() )3. 적절한 Weight 초기화
일부 방법들은 기울기 흐름(gradient flow)이 안정적으로 유지되도록 초기 가중치를 설정합니다.
- Xavier(Glorot) 초기화: tanh 함수에 적합합니다.
- He 초기화: ReLU 함수에 적합
PyTorch 예제:
torch.nn.init.kaiming_normal_(layer.weight, nonlinearity='relu')4. Residual Connections (Skip Connections) 사용
ResNet 이나 유사 아키텍처에서 사용:
- 스킵 연결(Skip connections) 은 기울기가 층을 가로질러 직접 흐를 수 있도록 해줍니다.
- 이로써 기울기 소실(vanishing gradient) 문제와 기울기 폭발(exploding gradient) 문제를 해결할 수 있습니다.
개념: 아래와 같이 직접 함수를 계산하는 대신
x = F(x)
이전 레이어의 결과 값과의 합을 계산한다. 수식은 합으로 표현되나 개념상 'residual'이 의미하는 것처럼 차이값을 계산하는 것임:
x = x + F(x)
PyTorch 예제:
class ResidualBlock(nn.Module):
def __init__(self, dim):
super().__init__()
self.linear = nn.Linear(dim, dim)
def forward(self, x):
return x + F.relu(self.linear(x))5. 다른 방법들
- 얕은 네트웍 사용
- 혹은 pretrained 모델을 이용한 파인 튜닝
결론
기울기 소실은 깊은 신경망에서 흔히 발생하는 문제로, 다양한 원인과 함께 성능 저하를 초래합니다. 하지만 ReLU, 배치 정규화, 잔차 연결 등 다양한 기법을 통해 이를 효과적으로 해결할 수 있습니다. 딥러닝 모델을 설계할 때 이러한 문제를 사전에 인식하고 적절한 대책을 세우는 것이 중요합니다.
참고자료
- Y. Bengio et al., "Learning long-term dependencies with gradient descent is difficult", IEEE Transactions on Neural Networks (1994)
- K. He et al., "Deep Residual Learning for Image Recognition", CVPR (2016)
- S. Ioffe and C. Szegedy, "Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift", ICML (2015)
- PyTorch 공식 문서: https://pytorch.org/docs/stable/nn.html
'AI' 카테고리의 다른 글
| 정보 이론과 정보 병목 완벽 가이드 (0) | 2025.04.21 |
|---|---|
| 딥러닝 활성화 함수 (Activation Functions) 완벽 가이드 (0) | 2025.04.21 |
| 딥러닝에서 특성 정규화 (Feature Normalization) 기법의 중요성 (0) | 2025.04.21 |
| CNN에서 Convolution(합성곱) 연산자 역할과 동작 원리 정리 (0) | 2025.04.21 |
| 딥러닝 모델 학습 시 Overfitting 대 Underfitting (0) | 2025.04.20 |



