CNN에서 Convolution(합성곱) 연산자 역할과 동작 원리 정리

합성곱 층(Convolution Layer) 이란?

합성곱 층은 합성곱 신경망(CNNs) 의 기본 구성 요소입니다. 주로 이미지 데이터를 처리하는 데 사용됩니다.

완전 연결층(fully connected layer)처럼 입력의 모든 픽셀을 모든 뉴런에 연결하는 대신, 합성곱 층은 작은 필터(커널)를 이미지 위에 슬라이딩하며 엣지(edge), 텍스처(texture), 패턴(pattern)과 같은 특성(features)을 추출합니다.

---

주요 용어들

• 입력(Input): 이미지 또는 특징맵 (예, 6X6 픽셀).
• 커널(Kernel): 이미지 위를 이동하는 작은 행렬 (예, 3X3 or 5X5).
• 스트라이드(Stride): 필터가 한 번에 이동하는 단계 수.
• 패딩(Padding): 출력 크기를 조절하기 위해 이미지 주위에 추가하는 여분의 픽셀.
• 피처맵(Feature Map): 합성곱 연산의 결과.

---

합성곱이 어떻게 작동하는지(예시와 함께)

패딩 없이, 스트라이드가 1인 예시를 통해 알아봅시다.

1. 입력: 6x6 Matrix

Input:
[ [9, 4, 1, 6, 5],
  [1, 1, 1, 0, 2],
  [1, 2, 1, 1, 3],
  [2, 1, 0, 3, 0],
  [1, 4, 2, 5, 6] ]

2. 커널: 3x3

Kernel:
[ [1, 2, 0],
  [0, 1, 4],
  [1, 0, 1] ]

 

3. 합성곱 연산 (3X3)

각 위치에서:

• 겹치는 숫자들을 곱한다.
• 그리고 그 결과들을 더한다.

왼쪽 위 모서리 예제 (처음 3X3 영역):

입력 조각:
[ [9, 1, 1],
  [1, 1, 1],
  [1, 2, 1] ]

계산:
9*1 + 1*2 + 1*0 +
1*0 + 1*1 + 1*4 +
1*1 + 2*0 + 1*1
= 9 + 2 + 0 + 0 + 1 + 4 + 1 + 0 + 1 = 24

**이 필터를 전체 입력에 걸쳐 슬라이딩하여 출력 특징 맵을 생성합니다.

Captured from Fuhg, J.N., Karmarkar, A., Kadeethum, T.  et al.  Deep convolutional Ritz method: parametric PDE surrogates without labeled data.  Appl. Math. Mech.-Engl. Ed.   44 , 1151–1174 (2023). https://doi.org/10.1007/s10483-023-2992-6

 

---

출력 크기 수식

 

예제: 5x5 커널

동일 6x6 입력에 5x5 커널를 패딩없이 할 경우:

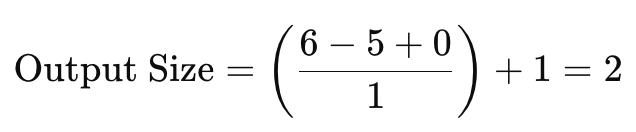
커널을 적용할 수 있는 위치는 2x2만큼입니다.

---

왜 완전 연결층 (FC layer) 대신 합성곱 층 (Convolution layer) ?

1. 파라미터 효율성

32x32 RGB image (즉, 32X32X3 = 3072 입력) 이미지가 주어질 때.

• 완전 연결층 (FC):
  모든 픽셀과 모든 뉴런이 연결됨.

       100개의 뉴런이 있을 경우: 파라미터=3072X100=307,200

• 합성곱 층 (3x3, 3 입력 채널, 32 필터):

      $필터\ 당\ 파라미터=3\times3\times3=27\ 전체=27\times32=864$

  ** 매우 적은 파라미터들 (307,200 → 864)!

2. 공간 계층

컨볼루션은 공간 정보를 유지합니다 (예: 인접한 픽셀은 관련이 있습니다), 반면 완전 연결층은 모든 것을 평탄화합니다..

---

합성곱 층의 파라미터 수는 어떻게 계산하는가?

각 필터에 대해서:

Parameters = $K \times K \times C_{in}$ + $1 \quad (\text{+1 for bias})$

다음 전체 필터들 수로 곱한다:

$\text{Total} = (K \times K \times C_{\text{in}} + 1) \times C_{\text{out}}​$

예제:

• 입력 채널 = 3 (RGB 이미지)
• 커널 크기 = 5x5
• 필터 수 = 64

{전체 파라미터 수} = (5 X 5 X 3 + 1) X 64 = (75 + 1) X 64 = 76 X 64 = 4864

---

MACs 은 어떻게 계산 하는가?

각 커널 적용 =

$K \times K \times C_{\text{in}} \text{ MACs per position}$

다음 두 항목의 곱:

• 아웃풋 위치의 수 $(H \times W)$
• 필터들 수

예제:

• 입력: 32x32x3
• 커널: 3x3
• 필터: 16
• 출력: 30x30 (패딩없음)

$\text{MACs} = 3 \times 3 \times 3 \times 30 \times 30 \times 16 = 388,800$

참고문헌

1. Fuhg, J.N., Karmarkar, A., Kadeethum, T.  et al.  Deep convolutional Ritz method: parametric PDE surrogates without labeled data.  Appl. Math. Mech.-Engl. Ed.   44 , 1151–1174 (2023). https://doi.org/10.1007/s10483-023-2992-6.